某人沿一条折线段组成的小路前进，从
到
，方位角（从正北方向顺时针转到
方向所成的角）是
，距离是3km；从到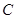
，方位角是110°，距离是3km；从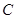到
，方位角是140°，距离是（
）km.试画出大致示意图，并计算出从A到D的方位角和距离（结果保留根号）.
相关试题
的值；（2）若
为钝角，求实数
，
．
时，若
上单调递减，求a的取值
范围；
：存在
，使得
的最大值，
的最小值；
满分12分) 
是R上的单调函数，且
，对于任意
都有
成立．
恒成立，求k的范围．
的反函数
的图象过点
．
的值；
，且
．
与x轴的两个交点
之间的距离为2，求b的值；
方程
的两个实数根分别在区间
内，求b的取值范
围．推荐套卷
某人沿一条折线段组成的小路前进，从到，方位角（从正北方向顺时针转到方向所成的角）是，距离是3km；从到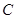，方位角是110°，距离是3km；从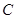到，方位角是140°，距离是（）km.试画出大致示意图，并计算出从A到D的方位角和距离（结果保留根号）.
粤公网安备 44130202000953号