某商店试销某种商品20天,获得如下数据:
| 日销售量(件) |
0 |
1 |
2 |
3 |
| 频数 |
1 |
5 |
9 |
5 |
试销结束后(假设该商品的日销售量的分布规律不变).设某天开始营业时由该商品3件,当天营业结束后检查存货,若发现存量少于2件,则当天进货补充至3件,否则不进货,将频率视为概率.
(1)求当天商店不进货的概率;
(2)记X为第二天开始营业时该商品视为件数,求X的分布列和数学期望.
相关知识点
推荐套卷
 P>0时,若对任意x>0,恒有f(x)≤0,求P的取值范围(2)证明:
P>0时,若对任意x>0,恒有f(x)≤0,求P的取值范围(2)证明: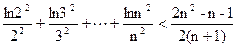 (n∈N
(n∈N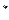 ,n≥2)
,n≥2)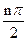 )an+sin
)an+sin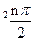 ,n=1、2、3…1)求a3、a4并求数列{an}的通项公式(2)设bn=
,n=1、2、3…1)求a3、a4并求数列{an}的通项公式(2)设bn=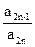 ,令 Sn=
,令 Sn=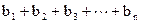 求Sn
求Sn x-
x- )-2cos2
)-2cos2 x+1(1)求f(x)的最小正周期(2)若函数y=g(x)与f(x)的图象关于直线x=1对称,求当x∈[0,
x+1(1)求f(x)的最小正周期(2)若函数y=g(x)与f(x)的图象关于直线x=1对称,求当x∈[0, ]时,y=g(x)的最大值
]时,y=g(x)的最大值 中,
中, ,
, 为其前
为其前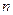 项的和,满足
项的和,满足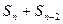 =
=
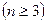 ,令
,令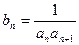 (Ⅰ)求数列
(Ⅰ)求数列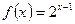 ,求证:
,求证: (Ⅲ)设
(Ⅲ)设 ,求证数列
,求证数列
 粤公网安备 44130202000953号
粤公网安备 44130202000953号