在平面直角坐标系xOy中，设曲线C1：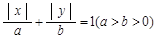
所围成的封闭图形的面积为
，曲线C1上的点到原点O的最短距离为
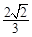．以曲线C1与坐标轴的交点为顶点的椭圆记为C2．
（1）求椭圆C2的标准方程；
（2）设AB是过椭圆C2中心O的任意弦，l是线段AB的垂直平分线．M是l上的点（与O不重合）．
①若MO＝2OA，当点A在椭圆C2上运动时，求点M的轨迹方程；
②若M是l与椭圆C2的交点，求△AMB的面积的最小值．
相关试题
.
是函数
的极值点,求
的值；
，
，函数
的图象与
轴的交点也在函数
的图象上，且在此点有公切线．
，
的值；
与
的大小．
，
，且
，其中A、B、C是
ABC的内角，
分别是角A，B，C的对边。
的取值范围；
为偶函数，且在区间
上是单调增函数
的解析式；
，其中
.若函数
仅在
处有极值，求
的取值范围.
的不等式
的解集为
，不等式
的解集为
．
，求
，求正数
的取值.推荐套卷
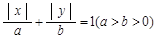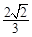在平面直角坐标系xOy中，设曲线C1：所围成的封闭图形的面积为，曲线C1上的点到原点O的最短距离为．以曲线C1与坐标轴的交点为顶点的椭圆记为C2．
（1）求椭圆C2的标准方程；
（2）设AB是过椭圆C2中心O的任意弦，l是线段AB的垂直平分线．M是l上的点（与O不重合）．
①若MO＝2OA，当点A在椭圆C2上运动时，求点M的轨迹方程；
②若M是l与椭圆C2的交点，求△AMB的面积的最小值．
粤公网安备 44130202000953号