一个圆柱形圆木的底面半径为1m，长为10m，将此圆木沿轴所在的平面剖成两个部分．现要把其中一个部分加工成直四棱柱木梁，长度保持不变，底面为等腰梯形
（如图所示，其中O为圆心，
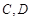在半圆上），设
，木梁的体积为V（单位：m3），表面积为S（单位：m2）．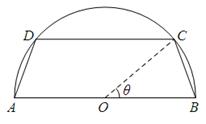
（1）求V关于θ的函数表达式；
（2）求
的值，使体积V最大；
（3）问当木梁的体积V最大时，其表面积S是否也最大？请说明理由．
是数列
的前
项和，
，
.
，求数列
的前
.
中，
，求数列
中，
，求数列
，求数列
时，
.
是以
为公比的等比数列，其首项为
，
，求数列
的前
项和为
，
；
，
的值；推荐套卷
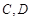一个圆柱形圆木的底面半径为1m，长为10m，将此圆木沿轴所在的平面剖成两个部分．现要把其中一个部分加工成直四棱柱木梁，长度保持不变，底面为等腰梯形（如图所示，其中O为圆心，在半圆上），设，木梁的体积为V（单位：m3），表面积为S（单位：m2）．
（1）求V关于θ的函数表达式；
（2）求的值，使体积V最大；
（3）问当木梁的体积V最大时，其表面积S是否也最大？请说明理由．
粤公网安备 44130202000953号