学习了函数的知识后,数学活动小组到文具店调研一种进价为每支2元的活动笔的销售情况。调查后发现,每支定价3元,每天能卖出100支,而且每支定价每下降0.1元,其销售量将增加10支。但是物价局规定,该活动笔每支的销售利润不能超过其进价的40%。设每支定价x元,每天的销售利润为y元。
(1)求每天的销售利润为y与每支定价x之间的函数关系式;
(2)如果要实现每天75元的销售利润,那么每支定价应为多少元?
(3)当每支定价为多少元时,可以使这种笔每天的销售利润最大?
相关知识点
推荐套卷
 ;
; .
.

 与
与 的和为零,先化简再求值:
的和为零,先化简再求值: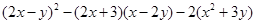 (本题4分)
(本题4分) 粤公网安备 44130202000953号
粤公网安备 44130202000953号