如图,圆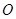 与直线
与直线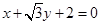 相切于点
相切于点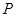 ,与
,与 正半轴交于点
正半轴交于点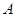 ,与直线
,与直线 在第一象限的交点为
在第一象限的交点为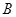 .点
.点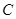 为圆
为圆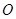 上任一点,且满足
上任一点,且满足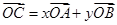 ,动点
,动点 的轨迹记为曲线
的轨迹记为曲线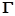 .
.
(1)求圆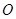 的方程及曲线
的方程及曲线 的轨迹方程;
的轨迹方程;
(2)若直线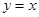 和
和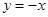 分别交曲线
分别交曲线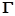 于点
于点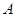 、
、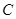 和
和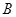 、
、 ,
,
求四边形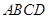 的周长;
的周长;
(3)已知曲线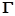 为椭圆,写出椭圆
为椭圆,写出椭圆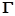 的对称轴、顶点坐标、范围和焦点坐标.
的对称轴、顶点坐标、范围和焦点坐标.
推荐套卷
如图,圆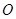 与直线
与直线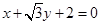 相切于点
相切于点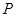 ,与
,与 正半轴交于点
正半轴交于点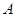 ,与直线
,与直线 在第一象限的交点为
在第一象限的交点为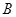 .点
.点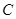 为圆
为圆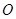 上任一点,且满足
上任一点,且满足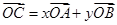 ,动点
,动点 的轨迹记为曲线
的轨迹记为曲线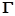 .
.
(1)求圆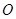 的方程及曲线
的方程及曲线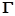 的轨迹方程;
的轨迹方程;
(2)若直线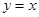 和
和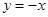 分别交曲线
分别交曲线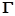 于点
于点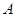 、
、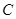 和
和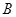 、
、 ,
,
求四边形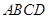 的周长;
的周长;
(3)已知曲线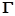 为椭圆,写出椭圆
为椭圆,写出椭圆 的对称轴、顶点坐标、范围和焦点坐标.
的对称轴、顶点坐标、范围和焦点坐标.