在已知函数f(x)＝Asin(ωx＋φ)，x∈R(其中A>0，ω>0,0<φ<
)的图象与x轴的交点中，相邻两个交点之间的距离为，且图象上一个最低点为M(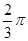
，－2)．
(1)求f(x)的解析式；
(2)当x∈[
，]时，求f(x)的值域．
相关试题
时，求不等式
的解集；
的解集包含
，求
的取值范围.
的极坐标方程是
，直线
的参数方程是
（
为参数）.
轴的交点是
为曲线
的最大值.
在二阶矩阵
的作用下变换为曲线
，
的值；
的逆矩阵
.
.
在
处取得极值，
、
的值；②存在
，使得不等式
成立，求
的最小值；
时，若
上是单调函数，求
）
为半圆，
为半圆直径，
为半圆圆心，且
，
为线段
的中点，已知
，曲线
过
在曲线
的值不变.
的直线
与曲线
两点，与
点，
，
证明：
为定值.
相关知识点
推荐套卷
在已知函数f(x)＝Asin(ωx＋φ)，x∈R(其中A>0，ω>0,0<φ<)的图象与x轴的交点中，相邻两个交点之间的距离为，且图象上一个最低点为M(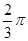，－2)．
(1)求f(x)的解析式；
(2)当x∈[，]时，求f(x)的值域．
粤公网安备 44130202000953号