为调查乘客的候车情况，公交公司在某站台的60名候车乘客中随机抽取15人，将他们的候车时间（单位：分钟）作为样本分成5组，如下表所示：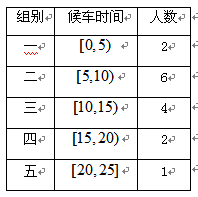
（1）估计这60名乘客中候车时间少于10分钟的人数；
（2）若从上表第三、四组的6人中随机抽取2人作进一步的问卷调查，求抽到的两人恰好来自不同组的概率．
相关试题
.
为等比数列，并由此求出
满足：
.试求数列
，设
，数列
。
是等差数列；
的前n项和Sn；
一切正整数n恒成立，求实数m的取值范围。
的前
项和为
，数列
满足
，且
，
．
的表达式；
，求数列
的前
．
项和.
及
满足
求数列
.
的值；推荐套卷
为调查乘客的候车情况，公交公司在某站台的60名候车乘客中随机抽取15人，将他们的候车时间（单位：分钟）作为样本分成5组，如下表所示：
（1）估计这60名乘客中候车时间少于10分钟的人数；
（2）若从上表第三、四组的6人中随机抽取2人作进一步的问卷调查，求抽到的两人恰好来自不同组的概率．
粤公网安备 44130202000953号