某校要建一个面积为450平方米的矩形球场,要求球场的一面利用旧墙,其他各面用钢筋网围成,且在矩形一边的钢筋网的正中间要留一个3米的进出口(如图).设矩形的长为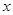 米,钢筋网的总长度为
米,钢筋网的总长度为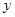 米.
米.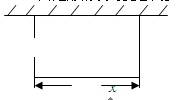
(1)列出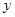 与
与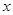 的函数关系式,并写出其定义域;
的函数关系式,并写出其定义域;
(2)问矩形的长与宽各为多少米时,所用的钢筋网的总长度最小?
(3)若由于地形限制,该球场的长和宽都不能超过25米,问矩形的长与宽各为多少米时,所用的钢筋网的总长度最小?
推荐套卷
某校要建一个面积为450平方米的矩形球场,要求球场的一面利用旧墙,其他各面用钢筋网围成,且在矩形一边的钢筋网的正中间要留一个3米的进出口(如图).设矩形的长为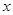 米,钢筋网的总长度为
米,钢筋网的总长度为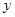 米.
米.
(1)列出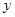 与
与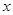 的函数关系式,并写出其定义域;
的函数关系式,并写出其定义域;
(2)问矩形的长与宽各为多少米时,所用的钢筋网的总长度最小?
(3)若由于地形限制,该球场的长和宽都不能超过25米,问矩形的长与宽各为多少米时,所用的钢筋网的总长度最小?