已知离心率为
的椭圆的顶点恰好是双曲线的左右焦点，点是椭圆上不同于的任意一点，设直线的斜率分别为.
（1）求椭圆的标准方程；
（2）当，在焦点在轴上的椭圆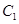
上求一点Q，使该点到直线（
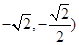的距离最大。
（3）试判断乘积“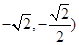（”的值是否与点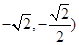（的位置有关，并证明你的结论；
相关试题
，
，
，求
；
，求实数
的取值范围。
的顶点在原点，始边与
轴的非负半轴重合，终边经过点
，
的值。
，求
的值。
是定义域在
上的不恒为零的函数，且对于任意非零实数
满足
.
与
的值；
的奇偶性；
上单调递减，求不等式
的解集.
在定义域
上是增函数且为奇函数，且
，求实数
的取值范围.
，求
的取值范围.相关知识点
推荐套卷
已知离心率为的椭圆的顶点恰好是双曲线的左右焦点，点是椭圆上不同于的任意一点，设直线的斜率分别为.
（1）求椭圆的标准方程；
（2）当，在焦点在轴上的椭圆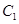上求一点Q，使该点到直线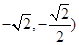（的距离最大。
（3）试判断乘积“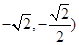（”的值是否与点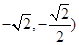（的位置有关，并证明你的结论；
粤公网安备 44130202000953号