从某校高三上学期期末数学考试成绩中，随机抽取了
名学生的成绩得到频率分布直方图如下：
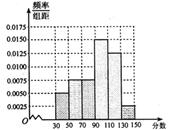
（1）根据频率分布直方图，估计该校高三学生本次数学考试的平均分；
（2）若用分层抽样的方法从分数在
和
的学生中共抽取
人，该人中成绩在的有几人？
（3）在（2）中抽取的人中，随机抽取
人，求分数在和各
人的概率．
是定义在
上的减函数，并且满足
，且
．
的值； 
，求
的取值范围．
,
，
，且
,求
的取值范围．
时，求函数的最大值和最小值；
的取值范围，使得函数
在区间
上是单调函数．
，
，
，求实数
的值．
，其中
，求函数
的最大值和最小值，并求出相应
的值．相关知识点
推荐套卷
从某校高三上学期期末数学考试成绩中，随机抽取了名学生的成绩得到频率分布直方图如下：
（1）根据频率分布直方图，估计该校高三学生本次数学考试的平均分；
（2）若用分层抽样的方法从分数在和的学生中共抽取人，该人中成绩在的有几人？
（3）在（2）中抽取的人中，随机抽取人，求分数在和各人的概率．
粤公网安备 44130202000953号