甲、乙两人破译一密码,它们能破译的概率分别为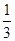 和
和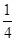 ,试求:
,试求:
(1)两人都能破译的概率;
(2)两人都不能破译的概率;
(3)恰有一人能破译的概率;
(4)至多有一人能破译的概率;
(5)若要使破译的概率为99%,至少需要多少乙这样的人?
相关知识点
推荐套卷
甲、乙两人破译一密码,它们能破译的概率分别为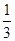 和
和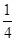 ,试求:
,试求:
(1)两人都能破译的概率;
(2)两人都不能破译的概率;
(3)恰有一人能破译的概率;
(4)至多有一人能破译的概率;
(5)若要使破译的概率为99%,至少需要多少乙这样的人?