如图,已知AE=CF,∠DAF=∠BCE,AD=CB.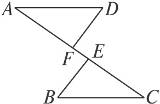
(1)问:△ADF与△CBE全等吗?请说明理由.
(2)如果将△BEC沿CA边方向平行移动,可有图中3幅图,如上面的条件不变,结论仍成立吗?请选择一幅图说明理由.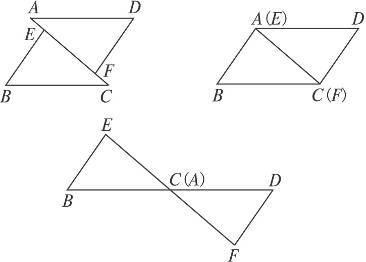
相关知识点
推荐套卷
如图,已知AE=CF,∠DAF=∠BCE,AD=CB.
(1)问:△ADF与△CBE全等吗?请说明理由.
(2)如果将△BEC沿CA边方向平行移动,可有图中3幅图,如上面的条件不变,结论仍成立吗?请选择一幅图说明理由.