已知椭圆 的焦距为2,且过点
的焦距为2,且过点 .
.
(1)求椭圆C的方程;
(2)设椭圆C的左右焦点分别为 ,
,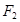 ,过点
,过点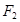 的直线
的直线 与椭圆C交于
与椭圆C交于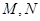 两点.
两点.
①当直线 的倾斜角为
的倾斜角为 时,求
时,求 的长;
的长;
②求 的内切圆的面积的最大值,并求出当
的内切圆的面积的最大值,并求出当 的内切圆的面积取最大值时直线
的内切圆的面积取最大值时直线 的方程.
的方程.
推荐套卷
已知椭圆 的焦距为2,且过点
的焦距为2,且过点 .
.
(1)求椭圆C的方程;
(2)设椭圆C的左右焦点分别为 ,
,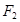 ,过点
,过点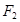 的直线
的直线 与椭圆C交于
与椭圆C交于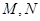 两点.
两点.
①当直线 的倾斜角为
的倾斜角为 时,求
时,求 的长;
的长;
②求 的内切圆的面积的最大值,并求出当
的内切圆的面积的最大值,并求出当 的内切圆的面积取最大值时直线
的内切圆的面积取最大值时直线 的方程.
的方程.