如图，在平面直角坐标系xOy中，椭圆C：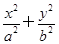
＝1(a＞b＞0)的离心率为
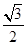，以原点为圆心，椭圆C的短半轴长为半径的圆与直线x－y＋2＝0相切．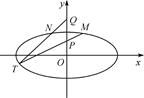
(1)求椭圆C的方程；
(2)已知点P(0，1)，Q(0，2)．设M、N是椭圆C上关于y轴对称的不同两点，直线PM与QN相交于点T，求证：点T在椭圆C上．
相关试题
；
的值。
前n项和为
满足：
，k为常数）
，求数列
的前n项和为
；
与
的大小。
，
与函数
,
的图像都相切，且与函数
在其定义域内为单调函数，求实数P的取值范围
，
，求△ABC的面积。
且
，
与
的夹角为
的最小值。推荐套卷
如图，在平面直角坐标系xOy中，椭圆C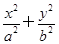：＝1(a＞b＞0)的离心率为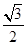，以原点为圆心，椭圆C的短半轴长为半径的圆与直线x－y＋2＝0相切．
(1)求椭圆C的方程；
(2)已知点P(0，1)，Q(0，2)．设M、N是椭圆C上关于y轴对称的不同两点，直线PM与QN相交于点T，求证：点T在椭圆C上．
粤公网安备 44130202000953号