如图，正方形CDEF内接于椭圆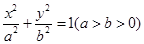
，且它的四条边与坐标轴平行，正方形GHPQ的顶点G,H在椭圆上，顶点P，Q在正方形的边EF上．且CD=2PQ=
．
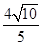(1)求椭圆的方程；
(2)已知点M(2,1)，平行于OM的直线l在y轴上的截距为m(m:≠0)，l交椭圆于A,B两个不同点，求证：直线MA，MB与x轴始终围成一个等腰三角形．
相关试题
，
的图像；（2）解不等式
。
是定义在
上的减函数，并且满足
，
，
的值， （2）如果
，求x的取值范围。
是定义在R上的函数，
，
。
.
上画出函数
的图像；
时，求证：在区间
上，
的图像位于函数
，（1）求函数的定义域；（2）求
的单调区间；推荐套卷
如图，正方形CDEF内接于椭圆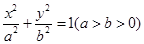，且它的四条边与坐标轴平行，正方形GHPQ的顶点G,H在椭圆上，顶点P，Q在正方形的边EF上．且CD=2PQ=．
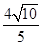(1)求椭圆的方程；
(2)已知点M(2,1)，平行于OM的直线l在y轴上的截距为m(m:≠0)，l交椭圆于A,B两个不同点，求证：直线MA，MB与x轴始终围成一个等腰三角形．
粤公网安备 44130202000953号