如图,直三棱柱ABC
A′B′C′,∠BAC=90°,AB=AC=
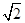,AA′=1,点M,N分别为
A′B和B′C′的中点.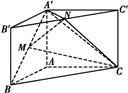
(1)证明:MN∥平面A′ACC′;
(2)求三棱锥A′MNC的体积.(锥体体积公式V=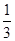
Sh,其中S为底面面积,h为高)
相关试题
的单调递增区间；
,求
，其中常数
．
，求函数
的单调递增区间；
，不等式
在
上恒成立，求实数
的取值范围.
在
处取得极值为
.
的值；
的方程
在
有两个不同的解，求实数
的取值范围.
（k∈R）为偶函数．
,若函数f（x）与g（x）图像有且只有一个公共点，求实数a的取值范围。
过点
，实数
满足
。命题Q：实数
。且
为真，求实数相关知识点
推荐套卷
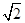如图,直三棱柱ABCA′B′C′,∠BAC=90°,AB=AC=,AA′=1,点M,N分别为
A′B和B′C′的中点.
(1)证明:MN∥平面A′ACC′;
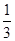(2)求三棱锥A′MNC的体积.(锥体体积公式V=Sh,其中S为底面面积,h为高)
粤公网安备 44130202000953号