如图所示,已知圆C与y轴相切于点T(0,2),与x轴正半轴相交于两点M,N(点M在点N的右侧),且|MN|=3,已知椭圆D: +
+ =1(a>b>0)的焦距等于2|ON|,且过点(
=1(a>b>0)的焦距等于2|ON|,且过点(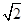 ,
,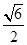 ).
).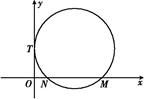
(1)求圆C和椭圆D的方程;
(2)若过点M斜率不为零的直线l与椭圆D交于A、B两点,求证:直线NA与直线NB的倾斜角互补.
推荐套卷
如图所示,已知圆C与y轴相切于点T(0,2),与x轴正半轴相交于两点M,N(点M在点N的右侧),且|MN|=3,已知椭圆D: +
+ =1(a>b>0)的焦距等于2|ON|,且过点(
=1(a>b>0)的焦距等于2|ON|,且过点(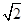 ,
,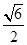 ).
).
(1)求圆C和椭圆D的方程;
(2)若过点M斜率不为零的直线l与椭圆D交于A、B两点,求证:直线NA与直线NB的倾斜角互补.