如图,椭圆的中心为原点O,长轴在x轴上,离心率e=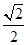 ,过左焦点F1作x轴的垂线交椭圆于A、A′两点,
,过左焦点F1作x轴的垂线交椭圆于A、A′两点,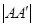 =4.
=4.
(1)求该椭圆的标准方程;
(2)取平行于y轴的直线与椭圆相交于不同的两点P、P′,过P、P′作圆心为Q的圆,使椭圆上的其余点均在圆Q外.求△PP′Q的面积S的最大值,并写出对应的圆Q的标准方程.
推荐套卷
如图,椭圆的中心为原点O,长轴在x轴上,离心率e=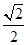 ,过左焦点F1作x轴的垂线交椭圆于A、A′两点,
,过左焦点F1作x轴的垂线交椭圆于A、A′两点,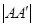 =4.
=4.
(1)求该椭圆的标准方程;
(2)取平行于y轴的直线与椭圆相交于不同的两点P、P′,过P、P′作圆心为Q的圆,使椭圆上的其余点均在圆Q外.求△PP′Q的面积S的最大值,并写出对应的圆Q的标准方程.