在平面直角坐标系xOy中,F是抛物线C:x2=2py(p>0)的焦点,M是抛物线C上位于第一象限内的任意一点,过M,F,O三点的圆的圆心为Q,点Q到抛物线C的准线的距离为 .
.
(1)求抛物线C的方程;
(2)是否存在点M,使得直线MQ与抛物线C相切于点M?若存在,求出点M的坐标;若不存在,说明理由.
(3)若点M的横坐标为 ,直线l:y=kx+
,直线l:y=kx+ 与抛物线C有两个不同的交点A,B,l与圆Q有两个不同的交点D,E,求当
与抛物线C有两个不同的交点A,B,l与圆Q有两个不同的交点D,E,求当 ≤k≤2时,|AB|2+|DE|2的最小值.
≤k≤2时,|AB|2+|DE|2的最小值.
相关知识点
推荐套卷
 年的年平均污水处理费用
年的年平均污水处理费用 (万元);
(万元); ,
, ,函数
,函数
 的最小正周期;
的最小正周期; 中,a, b, c分别是角A, B, C的对边,且
中,a, b, c分别是角A, B, C的对边,且 ,
, ,
, ,且
,且 ,求a, b的值.
,求a, b的值.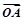 、
、 、
、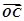 满足
满足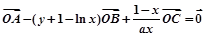 ,(O不在直线l上
,(O不在直线l上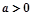 )
) 的表达式;
的表达式; 在
在 上为增函数,求a的范围;
上为增函数,求a的范围; 时,求证:
时,求证: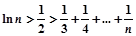 对
对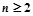 的正整数n成立.
的正整数n成立.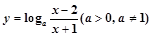 的定义域为
的定义域为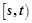 ,值域为
,值域为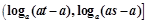 ,
, ;
;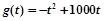 ,其中t是产品售出的数量,且
,其中t是产品售出的数量,且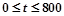 (利润=销售收入
(利润=销售收入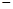 成本).
成本). 的解析式;
的解析式; 粤公网安备 44130202000953号
粤公网安备 44130202000953号