如图，椭圆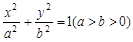
过点P(1, 
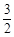)，其左、右焦点分别为F1,F2,离心率e＝
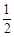,M,N是直线x＝4上的两个动点，且
·
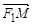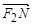＝0.
（1）求椭圆的方程；
（2）求|MN|的最小值；
（3）以MN为直径的圆C是否过定点？请证明你的结论。
相关试题
的奇偶性；(Ⅱ)求
成立的实数a的取值范围.
.
，（a¹0,a、bÎR）恒成立，求实数x的范围.
.
是（1）中曲线C上的动点，求
的取值范围.推荐套卷
如图，椭圆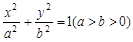过点P(1, 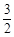)，其左、右焦点分别为F1,F2,离心率e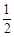＝,M,N是直线x＝4上的两个动点，且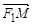·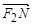＝0.
（1）求椭圆的方程；
（2）求|MN|的最小值；
（3）以MN为直径的圆C是否过定点？请证明你的结论。
粤公网安备 44130202000953号