如图，在四棱锥O—ABCD中，底面ABCD是边长为1的正方形，OA⊥底面ABCD，OA＝2，M为OA中点。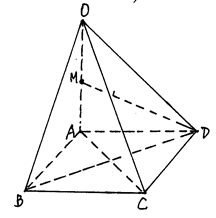
（1）求证：直线BD⊥平面OAC；
（2）求直线MD与平面OAC所成角的大小；
（3）求点A到平面OBD的距离。
相关试题
与一次函数
的图象交于点
的值；
，
，求这个函数的解析式.
的单调区间；
，使函数
在
处取得最小值，试求
的最大值.相关知识点
推荐套卷
如图，在四棱锥O—ABCD中，底面ABCD是边长为1的正方形，OA⊥底面ABCD，OA＝2，M为OA中点。
（1）求证：直线BD⊥平面OAC；
（2）求直线MD与平面OAC所成角的大小；
（3）求点A到平面OBD的距离。
粤公网安备 44130202000953号