定义在D上的函数f(x)，如果满足：对任意x∈D，存在常数M>0，都有|f(x)|≤M成立，则称f(x)是D上的有界函数，其中M称为函数f(x)的上界．已知函数f(x)＝1＋a·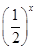
＋
.
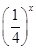(1)当a＝1时，求函数f(x)在(－∞，0)上的值域，并判断函数f(x)在(－∞，0)上是否为有界函数，请说明理由；
(2)若函数f(x)在[0，＋∞)上是以3为上界的有界函数，求实数a的取值范围．
上的函数
是减函数，且是奇函数，若
，求实数
的范围。
在(0,1)上是减函数．
，求
。
的值域。
求
的值.推荐套卷
定义在D上的函数f(x)，如果满足：对任意x∈D，存在常数M>0，都有|f(x)|≤M成立，则称f(x)是D上的有界函数，其中M称为函数f(x)的上界．已知函数f(x)＝1＋a·＋.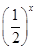
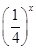(1)当a＝1时，求函数f(x)在(－∞，0)上的值域，并判断函数f(x)在(－∞，0)上是否为有界函数，请说明理由；
(2)若函数f(x)在[0，＋∞)上是以3为上界的有界函数，求实数a的取值范围．
粤公网安备 44130202000953号