已知f(x)＝xlnx，g(x)＝－x2＋ax－3.
(1)求函数f(x)在[t，t＋2](t>0)上的最小值；
(2)对一切x∈(0，＋∞)，2f(x)≥g(x)恒成立，求实数a的取值范围；
(3)证明对一切x∈(0，＋∞)，都有lnx>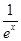
－
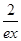成立．
的不等式
．
的不等式
．
满足：
公比
，数列
的前
项和为
，且
（
）．
和
；
，证明：
．
分别为
三个内角
的对边，且满足
．
的大小；
的最大值．
是公差为2的等差数列，且
成等比数列．
，记数列
的前项和为
，求证：
．推荐套卷
已知f(x)＝xlnx，g(x)＝－x2＋ax－3.
(1)求函数f(x)在[t，t＋2](t>0)上的最小值；
(2)对一切x∈(0，＋∞)，2f(x)≥g(x)恒成立，求实数a的取值范围；
(3)证明对一切x∈(0，＋∞)，都有lnx>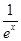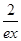－成立．
粤公网安备 44130202000953号