已知两条直线l1：y＝m和l2：y＝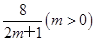
，l1与函数y＝|log2x|的图象从左至右相交于点A、B，l2与函数y＝|log2x|的图象从左至右相交于点C、D.记线段AC和BD在x轴上的投影长度分别为a、b.当m变化时，求
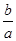的最小值．
相关试题
已知向量
＝(3，－4)，
＝(6，－3)，
＝(5－m，－3－m)．
（1）若点A，B，C不能构成三角形，求实数m满足的条件；
若△ABC为直角三角形，求实数m的值．
是三内角对应的三边，已知
．（1）求角A的大小；（2）若
＝
,且△ABC的面积为
,求
的值．
定义在
上，对任意的
，
，且
.
，并证明：
；
.设向量
，对任意
，
恒成立，求实数
的取值范围.
的前
项和为
，满足
，且
恰为等比数列
的前三项.
的前
.推荐套卷
已知两条直线l1：y＝m和l2：y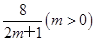＝，l1与函数y＝|log2x|的图象从左至右相交于点A、B，l2与函数y＝|log2x|的图象从左至右相交于点C、D.记线段AC和BD在x轴上的投影长度分别为a、b.当m变化时，求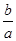的最小值．
已知向量＝(3，－4)，＝(6，－3)，＝(5－m，－3－m)．
（1）若点A，B，C不能构成三角形，求实数m满足的条件；
若△ABC为直角三角形，求实数m的值．
粤公网安备 44130202000953号