已知函数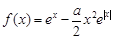
．
（Ⅰ）若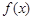
是
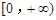上是增函数，求实数a的取值范围；
（Ⅱ）证明：当a≥1时，证明不等式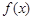≤x+1对x∈R恒成立；
（Ⅲ）对于在(0，1)中的任一个常数a，试探究是否存在x0>0，使得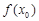
>x0+1成立？如果存在，请求出符合条件的一个x0；如果不存在，请说明理由．
，A=300，则角C及b.
为两个互相垂直的单位向量，求
是两个垂直的单位向量，且
（２）若
的值。
满足
求
夹角为
， 
的值。推荐套卷
已知函数．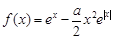
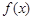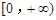（Ⅰ）若是上是增函数，求实数a的取值范围；
（Ⅱ）证明：当a≥1时，证明不等式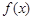≤x+1对x∈R恒成立；
（Ⅲ）对于在(0，1)中的任一个常数a，试探究是否存在x0>0，使得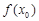>x0+1成立？如果存在，请求出符合条件的一个x0；如果不存在，请说明理由．
粤公网安备 44130202000953号