如图,在平行四边形ABCD中,AB=5,BC=10,F为AD的中点,CE⊥AB于E,设∠ABC=α(60°≤α<90°).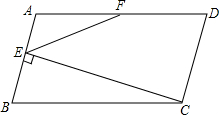
(1)当α=60°时,求CE的长;
(2)当60°<α<90°时,
①是否存在正整数k,使得∠EFD=k∠AEF?若存在,求出k的值;若不存在,请说明理由.
②连接CF,当CE2-CF2取最大值时,求tan∠DCF的值.
相关知识点
推荐套卷
如图,在平行四边形ABCD中,AB=5,BC=10,F为AD的中点,CE⊥AB于E,设∠ABC=α(60°≤α<90°).
(1)当α=60°时,求CE的长;
(2)当60°<α<90°时,
①是否存在正整数k,使得∠EFD=k∠AEF?若存在,求出k的值;若不存在,请说明理由.
②连接CF,当CE2-CF2取最大值时,求tan∠DCF的值.