设A，B分别是直线y＝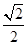
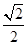x和y＝－x上的动点，且|AB|＝
，设O为坐标原点，动点P满足
＝
＋
.
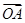(1)求点P的轨迹方程；
(2)过点(
，0)作两条互相垂直的直线l1，l2，直线l1，l2与点P的轨迹的相交弦分别为CD，EF，设CD，EF的弦中点分别为M，N，求证：直线MN恒过一个定点．
+
+
+
+
+…+
的值.推荐套卷
设A，B分别是直线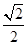y＝x和y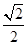＝－x上的动点，且|AB|＝，设O为坐标原点，动点P满足＝＋.
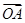(1)求点P的轨迹方程；
(2)过点(，0)作两条互相垂直的直线l1，l2，直线l1，l2与点P的轨迹的相交弦分别为CD，EF，设CD，EF的弦中点分别为M，N，求证：直线MN恒过一个定点．
粤公网安备 44130202000953号