椭圆C: =1(a>b>0)的左、右焦点分别是F1、F2,离心率为
=1(a>b>0)的左、右焦点分别是F1、F2,离心率为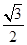 ,过F1且垂直于x轴的直线被椭圆C截得的线段长为1.
,过F1且垂直于x轴的直线被椭圆C截得的线段长为1.
(1)求椭圆C的方程;
(2)点P是椭圆C上除长轴端点外的任一点,过点P作斜率为k的直线l,使得l与椭圆C有且只有一个公共点.设直线PF1,PF2的斜率分别为k1,k2.若k≠0,试证明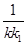 +
+ 为定值,并求出这个定值.
为定值,并求出这个定值.
推荐套卷
椭圆C: =1(a>b>0)的左、右焦点分别是F1、F2,离心率为
=1(a>b>0)的左、右焦点分别是F1、F2,离心率为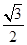 ,过F1且垂直于x轴的直线被椭圆C截得的线段长为1.
,过F1且垂直于x轴的直线被椭圆C截得的线段长为1.
(1)求椭圆C的方程;
(2)点P是椭圆C上除长轴端点外的任一点,过点P作斜率为k的直线l,使得l与椭圆C有且只有一个公共点.设直线PF1,PF2的斜率分别为k1,k2.若k≠0,试证明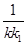 +
+ 为定值,并求出这个定值.
为定值,并求出这个定值.