已知中心在原点的椭圆C的一个焦点为F(4,0),长轴端点到较近焦点的距离为1,A(x1,y1),B(x2,y2)(x1≠x2)为椭圆上不同的两点.
(1)求椭圆C的方程.
(2)若x1+x2=8,在x轴上是否存在一点D,使|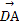
|=|
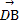|?若存在,求出D点的坐标;若不存在,说明理由.
相关试题
与圆的位置关系。
的三外顶点分别为
.
．
的最小值；
；
与
定义域上的任意实数
，若存在常数
，使得
和
都成立，则称直线
为函数
，
，推荐套卷
已知中心在原点的椭圆C的一个焦点为F(4,0),长轴端点到较近焦点的距离为1,A(x1,y1),B(x2,y2)(x1≠x2)为椭圆上不同的两点.
(1)求椭圆C的方程.
(2)若x1+x2=8,在x轴上是否存在一点D,使|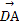|=||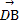?若存在,求出D点的坐标;若不存在,说明理由.
粤公网安备 44130202000953号