如图,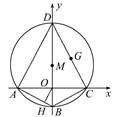
在平面直角坐标系中,方程为x2+y2+Dx+Ey+F=0的圆M的内接四边形ABCD的对角线AC和BD互相垂直,且AC和BD分别在x轴和y轴上.
(1)求证:F<0.
(2)若四边形ABCD的面积为8,对角线AC的长为2,且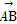
·
=0,求D2+E2-4F的值.
(3)设四边形ABCD的一条边CD的中点为G,OH⊥AB且垂足为H.试用平面解析几何的研究方法判断点O,G,H是否共线,并说明理由.
相关试题
的棱长为
，
分别是棱
的中点，
的体积。
中，底面
为矩形，
平面
为
的中点．
平面
;
求三棱锥
的体积。
中,
,
,点
为
中点．
平面
；
平面
；
，
，E为棱
的中点．
平面
；
的体积．
推荐套卷
如图,
在平面直角坐标系中,方程为x2+y2+Dx+Ey+F=0的圆M的内接四边形ABCD的对角线AC和BD互相垂直,且AC和BD分别在x轴和y轴上.
(1)求证:F<0.
(2)若四边形ABCD的面积为8,对角线AC的长为2,且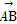·=0,求D2+E2-4F的值.
(3)设四边形ABCD的一条边CD的中点为G,OH⊥AB且垂足为H.试用平面解析几何的研究方法判断点O,G,H是否共线,并说明理由.
粤公网安备 44130202000953号