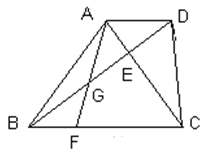
已知:r如图,在梯形ABCD中,AD∥BC,∠BCD=90°.对角线AC、BD相交于点E。且AC⊥BD。(1)求证:CD²=BC·AD;(2)点F是边BC上一点,连接AF,与BD相交于点G,如果∠BAF=∠DBF,求证: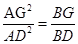 。
。
相关知识点
推荐套卷
已知:r如图,在梯形ABCD中,AD∥BC,∠BCD=90°.对角线AC、BD相交于点E。且AC⊥BD。(1)求证:CD²=BC·AD;(2)点F是边BC上一点,连接AF,与BD相交于点G,如果∠BAF=∠DBF,求证: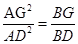 。
。
