已知:如图,抛物线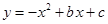 与
与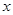 轴的负半轴相交于点
轴的负半轴相交于点 ,与
,与 轴相交于点
轴相交于点 (0,3),且∠
(0,3),且∠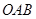 的余切值为
的余切值为 .
.
(1)求该抛物线的表达式,并写出顶点 的坐标;
的坐标;
(2)设该抛物线的对称轴为直线 ,点
,点 关于直线
关于直线 的对称点为
的对称点为 ,
,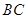 与直线
与直线 相交于点
相交于点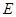 .点
.点 在直线
在直线 上,如果点
上,如果点 是△
是△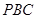 的重心,求点
的重心,求点 的坐标;
的坐标;
(3)在(2)的条件下,将(1)所求得的抛物线沿 轴向上或向下平移后顶点为点
轴向上或向下平移后顶点为点 ,写出平移后抛物线的表达式.点
,写出平移后抛物线的表达式.点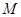 在平移后的抛物线上,且△
在平移后的抛物线上,且△ 的面积等于△
的面积等于△ 的面积的2倍,求点
的面积的2倍,求点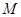 的坐标.
的坐标.
相关知识点
推荐套卷
 .延长BD交x轴于点C,过点D作DA⊥x轴,垂足为A,OA=4,OB=3.
.延长BD交x轴于点C,过点D作DA⊥x轴,垂足为A,OA=4,OB=3. (k>0)的图象上,求反比例函数的解析式.
(k>0)的图象上,求反比例函数的解析式.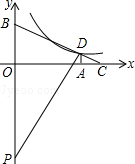


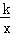 (x>0)的图象上,
(x>0)的图象上,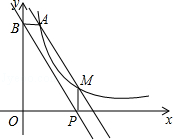
 粤公网安备 44130202000953号
粤公网安备 44130202000953号