已知a=(5 cos x,cos x),b=(sin x,2cos x),设函数f(x)=a·b+|b|2+
cos x,cos x),b=(sin x,2cos x),设函数f(x)=a·b+|b|2+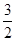 .
.
(1)当∈ 时,求函数f(x)的值域;
时,求函数f(x)的值域;
(2)当x∈ 时,若f(x)=8,求函数f
时,若f(x)=8,求函数f 的值;
的值;
(3)将函数y=f(x)的图象向右平移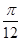 个单位后,再将得到的图象上各点的纵坐标向下平移5个单位,得到函数y=g(x)的图象,求函数g(x)的表达式并判断奇偶性.
个单位后,再将得到的图象上各点的纵坐标向下平移5个单位,得到函数y=g(x)的图象,求函数g(x)的表达式并判断奇偶性.
相关知识点
推荐套卷
已知a=(5 cos x,cos x),b=(sin x,2cos x),设函数f(x)=a·b+|b|2+
cos x,cos x),b=(sin x,2cos x),设函数f(x)=a·b+|b|2+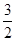 .
.
(1)当∈ 时,求函数f(x)的值域;
时,求函数f(x)的值域;
(2)当x∈ 时,若f(x)=8,求函数f
时,若f(x)=8,求函数f 的值;
的值;
(3)将函数y=f(x)的图象向右平移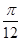 个单位后,再将得到的图象上各点的纵坐标向下平移5个单位,得到函数y=g(x)的图象,求函数g(x)的表达式并判断奇偶性.
个单位后,再将得到的图象上各点的纵坐标向下平移5个单位,得到函数y=g(x)的图象,求函数g(x)的表达式并判断奇偶性.