在四棱锥P－ABCD中，PA⊥平面ABCD，△ABC是正三角形，AC与BD的交点M恰好是AC的中点，又∠CAD＝30°，PA＝AB＝4，点N在线段PB上，且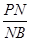
＝
.
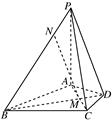
(1)求证：BD⊥PC；
(2)求证：MN∥平面PDC；
(3)设平面PAB∩平面PCD＝l，试问直线l是否与直线CD平行，请说明理由．
和直线
的交点
的坐标，及点
的距离。
；
；
的单调递增区间； 
求函数
的最值及对应的
在
的取值范围.
的方程
，求方程有实根的概率；
，求方程有实根的概率.
；
是第三象限角，且
，求
，求推荐套卷
在四棱锥P－ABCD中，PA⊥平面ABCD，△ABC是正三角形，AC与BD的交点M恰好是AC的中点，又∠CAD＝30°，PA＝AB＝4，点N在线段PB上，且＝.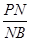
(1)求证：BD⊥PC；
(2)求证：MN∥平面PDC；
(3)设平面PAB∩平面PCD＝l，试问直线l是否与直线CD平行，请说明理由．
粤公网安备 44130202000953号