在平面直角坐标系中,已知向量a=(-1,2),又点A(8,0),B(n,t),C(ksinθ,t)(0≤θ≤ ).
).
(1)若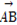 ⊥a,且|
⊥a,且|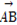 |=
|=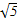 |
| |(O为坐标原点),求向量
|(O为坐标原点),求向量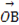 .
.
(2)若向量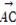 与向量a共线,当k>4,且tsinθ取最大值4时,求
与向量a共线,当k>4,且tsinθ取最大值4时,求 ·
·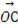 .
.
推荐套卷
在平面直角坐标系中,已知向量a=(-1,2),又点A(8,0),B(n,t),C(ksinθ,t)(0≤θ≤ ).
).
(1)若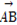 ⊥a,且|
⊥a,且|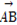 |=
|=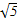 |
| |(O为坐标原点),求向量
|(O为坐标原点),求向量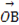 .
.
(2)若向量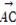 与向量a共线,当k>4,且tsinθ取最大值4时,求
与向量a共线,当k>4,且tsinθ取最大值4时,求 ·
·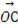 .
.