设f(x)＝ln(x2＋1)，g(x)＝
x2－.
(1)求F(x)＝f(x)－g(x)的单调区间，并证明对[－1，1]上的任意x1，x2，x3，都有F(x1)＋F(x2)>F(x3)；
(2)将y＝f(x)的图像向下平移a(a>0)个单位，同时将y＝g(x)的图像向上平移b(b>0)个单位，使它们恰有四个交点，求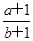
的取值范围．
相关试题
轴相切并与圆
相外切的动圆的圆心的轨迹方程。
，过P作直线
与圆相交于A、B，求弦AB中点的轨迹方程。
，求过点（1，
）的切线方程
，求过点P（3，1）圆的切线方程。
轴所得弦长为
；②被
轴分成两段圆弧，其弧长的比为
；③圆心到直线
：
的距离为
的圆的方程。
与已知圆
的交点，且在两坐标轴上的四个截距之和为8的圆的方程。推荐套卷
设f(x)＝ln(x2＋1)，g(x)＝x2－.
(1)求F(x)＝f(x)－g(x)的单调区间，并证明对[－1，1]上的任意x1，x2，x3，都有F(x1)＋F(x2)>F(x3)；
(2)将y＝f(x)的图像向下平移a(a>0)个单位，同时将y＝g(x)的图像向上平移b(b>0)个单位，使它们恰有四个交点，求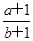的取值范围．
粤公网安备 44130202000953号