已知双曲线 的焦点与椭圆
的焦点与椭圆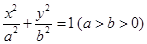 的焦点重合,且该椭圆的长轴长为
的焦点重合,且该椭圆的长轴长为 ,
, 是椭圆上的的动点.
是椭圆上的的动点.
(1)求椭圆标准方程;
(2)设动点 满足:
满足: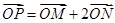 ,直线
,直线 与
与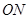 的斜率之积为
的斜率之积为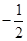 ,求证:存在定点
,求证:存在定点 ,
,
使得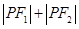 为定值,并求出
为定值,并求出 的坐标;
的坐标;
(3)若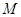 在第一象限,且点
在第一象限,且点 关于原点对称,点
关于原点对称,点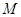 在
在 轴的射影为
轴的射影为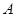 ,连接
,连接 并延长交椭圆于
并延长交椭圆于
点 ,求证:以
,求证:以 为直径的圆经过点
为直径的圆经过点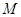 .
.
相关知识点
推荐套卷
已知双曲线 的焦点与椭圆
的焦点与椭圆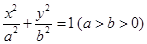 的焦点重合,且该椭圆的长轴长为
的焦点重合,且该椭圆的长轴长为 ,
, 是椭圆上的的动点.
是椭圆上的的动点.
(1)求椭圆标准方程;
(2)设动点 满足:
满足: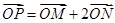 ,直线
,直线 与
与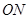 的斜率之积为
的斜率之积为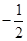 ,求证:存在定点
,求证:存在定点 ,
,
使得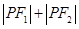 为定值,并求出
为定值,并求出 的坐标;
的坐标;
(3)若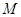 在第一象限,且点
在第一象限,且点 关于原点对称,点
关于原点对称,点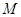 在
在 轴的射影为
轴的射影为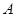 ,连接
,连接 并延长交椭圆于
并延长交椭圆于
点 ,求证:以
,求证:以 为直径的圆经过点
为直径的圆经过点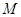 .
.