如图(1)，四边形ABCD中，E是BC的中点，DB＝2，DC＝1，BC＝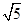
，AB＝AD＝
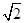.将图(1)沿直线BD折起，使得二面角ABDC为60°，如图(2)．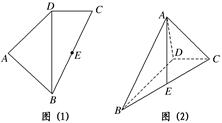
(1)求证：AE⊥平面BDC；
(2)求直线AC与平面ABD所成角的余弦值．
相关知识点
推荐套卷
如图(1)，四边形ABCD中，E是BC的中点，DB＝2，DC＝1，BC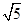＝，AB＝AD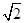＝.将图(1)沿直线BD折起，使得二面角ABDC为60°，如图(2)．
(1)求证：AE⊥平面BDC；
(2)求直线AC与平面ABD所成角的余弦值．
粤公网安备 44130202000953号