已知圆C1：x2＋y2－2y＝0，圆C2：x2＋(y＋1)2＝4的圆心分别为C1，C2，P为一个动点，且直线PC1，PC2的斜率之积为－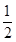
.
(1)求动点P的轨迹M的方程；
(2)是否存在过点A(2，0)的直线l与轨迹M交于不同的两点C，D，使得|C1C|＝|C1D|？若存在，求直线l的方程；若不存在，请说明理由．
相关试题
．
，
)
的最大值．
，其中
.
时，求不等式
的解集；
的解集为
，求
的值.
；
的值.推荐套卷
已知圆C1：x2＋y2－2y＝0，圆C2：x2＋(y＋1)2＝4的圆心分别为C1，C2，P为一个动点，且直线PC1，PC2的斜率之积为－.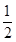
(1)求动点P的轨迹M的方程；
(2)是否存在过点A(2，0)的直线l与轨迹M交于不同的两点C，D，使得|C1C|＝|C1D|？若存在，求直线l的方程；若不存在，请说明理由．
粤公网安备 44130202000953号