已知数列{an}满足a1=a(a>0,a∈N*),a1+a2+…+an-pan+1=0(p≠0,p≠-1,n∈N*).
(1)求数列{an}的通项公式an;
(2)若对每一个正整数k,若将ak+1,ak+2,ak+3按从小到大的顺序排列后,此三项均能构成等差数列,且公差为dk.①求p的值及对应的数列{dk}.
②记Sk为数列{dk}的前k项和,问是否存在a,使得Sk<30对任意正整数k恒成立?若存在,求出a的最大值;若不存在,请说明理由.
相关知识点
推荐套卷
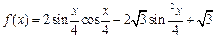
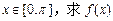 的值域;
的值域;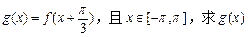 的增区间
的增区间 ,考虑到坚固性及用料,要求横断面的面
,考虑到坚固性及用料,要求横断面的面 积为
积为 ,记水渠深为x m,用料部分的周长(即渠底BC及两腰长的和)为y
,记水渠深为x m,用料部分的周长(即渠底BC及两腰长的和)为y m。
m。 时,横断面用料部分的周长最小?最小值是多少米?
时,横断面用料部分的周长最小?最小值是多少米?
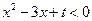 的解集为
的解集为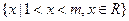 ;
;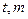 的值;
的值;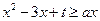 在
在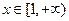 上恒成立,求实数
上恒成立,求实数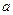 的最大值.
的最大值.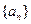 满足:
满足: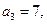
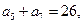
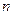 项和
项和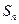 ;
;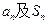 ;
;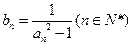 ,求数列
,求数列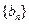 的前
的前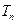 .
. 题12分)解不等式:
题12分)解不等式: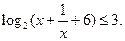
 粤公网安备 44130202000953号
粤公网安备 44130202000953号