形状如图所示的三个游戏盘中(图①是正方形，M，N分别是所在边中点，图②是半径分别为2和4的两个同心圆，O为圆心，图③是正六边形，点P为其中心)各有一个玻璃小球，依次摇动三个游戏盘后，将它们水平放置，就完成了一局游戏．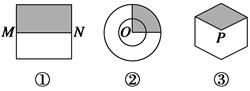
(1)一局游戏后，这三个盘中的小球都停在阴影部分的概率是多少？
(2)用随机变量X表示一局游戏后，小球停在阴影部分的事件数与小球没有停在阴影部分的事件数之差的绝对值，求随机变量X的分布列．
相关试题
试讨论
的单调性．
的顶点
，顶点
在直线
上；
求点
，且
，求角
，其中
.
，求
在
的最小值；
在定义域内既有极大值又有极小值，求实数
的取值范围；
，使得当
时，不等式
恒成立.
中
，
为线段
上一点，且
，线段
．
，
，试求线段
的长.
的定义域为
，且同时满足以下三个条件：①
；②对任意的
，都有
；③当
时总有
．
的值；
时，恒有
．推荐套卷
形状如图所示的三个游戏盘中(图①是正方形，M，N分别是所在边中点，图②是半径分别为2和4的两个同心圆，O为圆心，图③是正六边形，点P为其中心)各有一个玻璃小球，依次摇动三个游戏盘后，将它们水平放置，就完成了一局游戏．
(1)一局游戏后，这三个盘中的小球都停在阴影部分的概率是多少？
(2)用随机变量X表示一局游戏后，小球停在阴影部分的事件数与小球没有停在阴影部分的事件数之差的绝对值，求随机变量X的分布列．
粤公网安备 44130202000953号