定义在R上的函数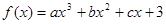
同时满足以下条件：
①
在(0,1)上是减函数，在(1，＋∞)上是增函数；
②
是偶函数；
③在x＝0处的切线与直线y＝x＋2垂直．
(1)求函数
的解析式；
(2)设g(x)＝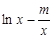
，若存在实数x∈[1，e]，使g(x)<，求实数m的取值范围。
在
上的最大值和最小值.
作曲线
的切线，求此切线的方程.
与直线
围成的平面图形的面积.
不可能成等差数列
, （1）求函数
的单调区间；
上的最小值是
，求
的值。推荐套卷
定义在R上的函数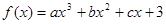同时满足以下条件：
①在(0,1)上是减函数，在(1，＋∞)上是增函数；
②是偶函数；
③在x＝0处的切线与直线y＝x＋2垂直．
(1)求函数的解析式；
(2)设g(x)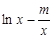＝，若存在实数x∈[1，e]，使g(x)<，求实数m的取值范围。
粤公网安备 44130202000953号