在平面直角坐标系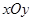 中,抛物线
中,抛物线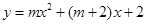 过点
过点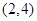 ,且与x轴交于A、B两点(点A在点B左侧),与y轴交于点C.点D的坐标为
,且与x轴交于A、B两点(点A在点B左侧),与y轴交于点C.点D的坐标为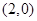 ,连接CA,CB,CD.
,连接CA,CB,CD.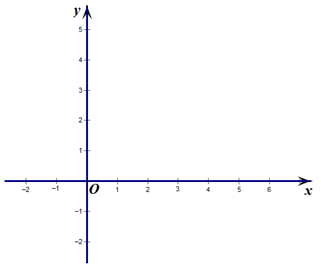
(1)求证: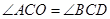 ;
;
(2)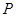 是第一象限内抛物线上的一个动点,连接DP交BC于点E.
是第一象限内抛物线上的一个动点,连接DP交BC于点E.
①当△BDE是等腰三角形时,直接写出点E的坐标;
②连接CP,当△CDP的面积最大时,求点E的坐标.
相关知识点
推荐套卷
在平面直角坐标系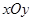 中,抛物线
中,抛物线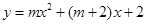 过点
过点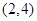 ,且与x轴交于A、B两点(点A在点B左侧),与y轴交于点C.点D的坐标为
,且与x轴交于A、B两点(点A在点B左侧),与y轴交于点C.点D的坐标为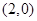 ,连接CA,CB,CD.
,连接CA,CB,CD.
(1)求证: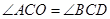 ;
;
(2)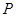 是第一象限内抛物线上的一个动点,连接DP交BC于点E.
是第一象限内抛物线上的一个动点,连接DP交BC于点E.
①当△BDE是等腰三角形时,直接写出点E的坐标;
②连接CP,当△CDP的面积最大时,求点E的坐标.