设袋子中装有a个红球，b个黄球，c个蓝球，且规定：取出一个红球得1分，取出一个黄球得2分，取出一个蓝球得3分．
(1)当a＝3，b＝2，c＝1时，从该袋子中任取(有放回，且每球取到的机会均等)2个球，记随机变量ξ为取出此2球所得分数之和，求ξ的分布列；
(2)从该袋子中任取(每球取到的机会均等)1个球，记随机变量η为取出此球所得分数．若E(η)＝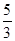
，D(η)＝
，求a∶b∶c.
得到曲线
的变化过程，并求出坐标伸缩变换.
.
.
，半径为3的圆的极坐标方程.推荐套卷
设袋子中装有a个红球，b个黄球，c个蓝球，且规定：取出一个红球得1分，取出一个黄球得2分，取出一个蓝球得3分．
(1)当a＝3，b＝2，c＝1时，从该袋子中任取(有放回，且每球取到的机会均等)2个球，记随机变量ξ为取出此2球所得分数之和，求ξ的分布列；
(2)从该袋子中任取(每球取到的机会均等)1个球，记随机变量η为取出此球所得分数．若E(η)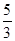＝，D(η)＝，求a∶b∶c.
粤公网安备 44130202000953号