如图，抛物线E：y2＝4x的焦点为F，准线l与x轴的交点为A.点C在抛物线E上，以C为圆心，|CO|为半径作圆，设圆C与准线l交于不同的两点M，N.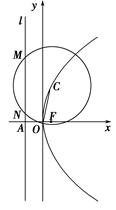
(1)若点C的纵坐标为2，求|MN|；
(2)若|AF|2＝|AM|·|AN|，求圆C的半径．
相关试题
：
与双曲线
：
相交于不同的
、
两点。
，使得以线段
为直径的圆经过坐标第原点？若存在，求出
．
的值；
时，求函数
的值域．相关知识点
推荐套卷
如图，抛物线E：y2＝4x的焦点为F，准线l与x轴的交点为A.点C在抛物线E上，以C为圆心，|CO|为半径作圆，设圆C与准线l交于不同的两点M，N.
(1)若点C的纵坐标为2，求|MN|；
(2)若|AF|2＝|AM|·|AN|，求圆C的半径．
粤公网安备 44130202000953号