已知四边形ABCD是菱形，∠BAD＝60°，四边形BDEF是矩形，平面BDEF⊥平面ABCD，G，H分别是CE，CF的中点．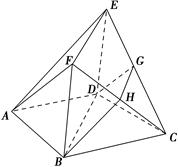
(1)求证：平面AEF∥平面BDGH
(2)若平面BDGH与平面ABCD所成的角为60°，求直线CF与平面BDGH所成的角的正弦值．
中，
中，
，求数列
项和
。
s2x+3sinx-1,(x
R)的最小值与最大值。
R
部分图象如图,求函数
的解析式
的简图相关知识点
推荐套卷
已知四边形ABCD是菱形，∠BAD＝60°，四边形BDEF是矩形，平面BDEF⊥平面ABCD，G，H分别是CE，CF的中点．
(1)求证：平面AEF∥平面BDGH
(2)若平面BDGH与平面ABCD所成的角为60°，求直线CF与平面BDGH所成的角的正弦值．
粤公网安备 44130202000953号