如图，在小山的东侧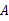
处有一热气球，以每分钟
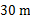的速度沿着仰角为60°的方向上升，20 min后升到
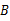处，这时热气球上的人发现在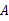的正西方向俯角为45°的
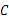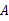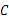处有一着火点，求热气球的升空点与着火点的距离（结果保留根号）.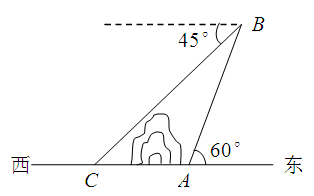
＝－
-[-5+（1-0.6
）
]相关知识点
推荐套卷
如图，在小山的东侧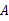处有一热气球，以每分钟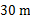的速度沿着仰角为60°的方向上升，20 min后升到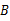处，这时热气球上的人发现在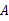的正西方向俯角为45°的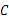处有一着火点，求热气球的升空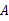点与着火点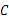的距离（结果保留根号）.
粤公网安备 44130202000953号