设椭圆M：
＝1(a>
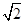)的右焦点为F1，直线l：x＝
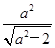与x轴交于点A，若
1＝2
(其中O为坐标原点)．
(1)求椭圆M的方程；
(2)设P是椭圆M上的任意一点，EF为圆N：x2＋(y－2)2＝1的任意一条直径(E，F为直径的两个端点)，求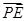
·
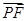的最大值．
相关试题
的首项
其中
，
令集合
.
，写出集合
中的所有的元素；
，且数列
的所有可能取值构成的集合；
.
时，求曲线
在点
处的切线方程；
的单调区间；
的取值范围.
，函数
的图象上的动点
在
轴上的射影为
，且点
的左侧.设
，
的面积为
.
的取值范围；
满足
.
，求数列
的前
项和公式.
中，
，
.
的值；
的值.推荐套卷
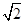设椭圆M：＝1(a>)的右焦点为F1，直线l：x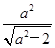＝与x轴交于点A，若1＝2 (其中O为坐标原点)．
(1)求椭圆M的方程；
(2)设P是椭圆M上的任意一点，EF为圆N：x2＋(y－2)2＝1的任意一条直径(E，F为直径的两个端点)，求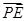·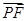的最大值．
粤公网安备 44130202000953号