在四棱锥P-ABCD中，底面ABCD是边长为1的正方形，且PA⊥平面ABCD.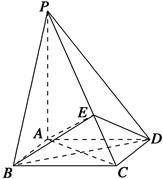
(1)求证：PC⊥BD；
(2)过直线BD且垂直于直线PC的平面交PC于点E，且三棱锥E-BCD的体积取到最大值．
①求此时四棱锥E-ABCD的高；
②求二面角A-DE-B的正弦值的大小．
的值，使圆
的直线方程．
的图象；
的单调递增区间．
的坐标；（2）过点
推荐套卷
在四棱锥P-ABCD中，底面ABCD是边长为1的正方形，且PA⊥平面ABCD.
(1)求证：PC⊥BD；
(2)过直线BD且垂直于直线PC的平面交PC于点E，且三棱锥E-BCD的体积取到最大值．
①求此时四棱锥E-ABCD的高；
②求二面角A-DE-B的正弦值的大小．
粤公网安备 44130202000953号